問題
Ⅲ－13 ある職場において不適合品の発生原因について調査し、以下のようなパレート図を作成した。現状の不適合品率が1.8%のとき、この図から読み取れる次の記述のうち、最も不適切なものはどれか。
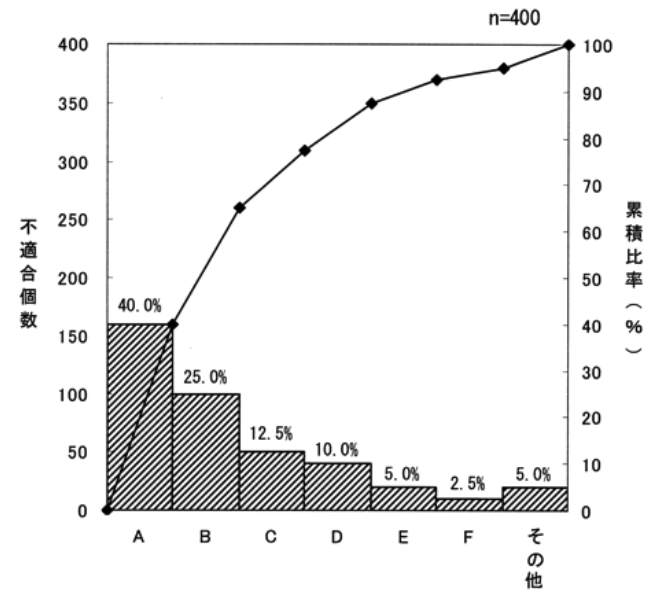
① 棒グラフは、その他を除いてA～F項目は不適合個数の降順に並んでいる。
② A, Bの2つの項目を解決すると全体の不適合個数の約65%が解決される。
③ A～D項目までを解決すると、不適合品率が約0.8%に減少する。
④ F項目を解決しても、全体の不適合個数の2.5%にしか影響しない。
⑤ C項目を解決すると、不適合品率が約1.6%となる。
解答
正解は 3 になります。
問題の背景と全体像
パレート図は、不適合品や問題点の発生原因を分析するために使用される品質管理のツールです。
この問題では、不適合品率が1.8%である職場のパレート図を基に、各記述の妥当性を検証し、不適切な記述を特定することが求められます。
パレート図の基本構造
- 棒グラフ: 各項目（A～F）の不適合個数を降順に並べたもの。
- 折れ線グラフ: 累積比率を示し、全体に対する各項目の影響度を視覚化。
- n=400: 全体の不適合個数が400個であることを示す。
各選択肢の徹底検証
選択肢① 「棒グラフは、その他を除いてA～F項目は不適合個数の降順に並んでいる」
- 適切性: 適切
- 解説:
棒グラフを見ると、A（40%）→B（25%）→C（12.5%）→D（10%）→E（5%）→F（2.5%）の順で不適合個数が降順に並んでいます。これはパレート図の基本的な構造です。
→ 適切
選択肢② 「A, Bの2つの項目を解決すると全体の不適合個数の約65%が解決される」
- 適切性: 適切
- 解説:
A項目（40%）とB項目（25%）を合わせると累積比率は65%となります。これにより、不適合個数の約65%が解決されることが読み取れます。
→ 適切
選択肢③ 「A～D項目までを解決すると、不適合品率が約0.8%に減少する」
- 適切性: 不適切
- 誤りの核心:
- 現状の不適合品率は1.8%。A～D項目までを解決すると累積比率は87.5%（40%+25%+12.5%+10%）。
- 不適合品率への影響は次式で計算されます：
減少後の不適合品率=1.8%×(1−0.875)=0.225%\text{減少後の不適合品率} = 1.8\% \times (1 – 0.875) = 0.225\%減少後の不適合品率=1.8%×(1−0.875)=0.225% - 記述では「約0.8%」とされていますが、実際には0.225%、大きく異なるため誤りです。
→ 不適切
選択肢④ 「F項目を解決しても、全体の不適合個数の2.5%にしか影響しない」
- 適切性: 適切
- 解説:
F項目の棒グラフを見ると、不適合個数は全体の2.5%。この項目のみを解決しても全体への影響は小さいことが確認できます。
→ 適切
選択肢⑤ 「C項目を解決すると、不適合品率が約1.6%となる」
- 適切性: 適切
- 解説:
C項目（12.5%）のみを解決した場合、不適合品率への影響は次式で計算されます：
減少後の不適合品率=1.8%×(1−0.125)=1.575%\text{減少後の不適合品率} = 1.8\% \times (1 – 0.125) = 1.575\%減少後の不適合品率=1.8%×(1−0.125)=1.575%- 記述では「約1.6%」とされており、ほぼ正確です。
→ 適切
問題の要点まとめ
正解：③
選択肢③が不適切な理由：A～D項目までを解決した場合、不適合品率は約0.225%となり、「約0.8%」という記述は誤りです。
試験対策ポイント
- パレート図では累積比率から各項目の影響度を読み取ることが重要。
- 不適合品率への影響は累積比率と現状値から計算する必要がある。
- 数値計算ミスや記述内容との整合性に注意する。
感想
うん、問題なく正解。
ちょちょっと電卓は叩きましたが。
品質管理がキモだよなあ、やっぱり。
この時の問題とほぼ同じでしたね、今回は。
だから問題なく今日は正解できたのかと納得。
関連記事Related articles
