問題
Ⅲ-16 ある部品の寸法規格は、53.02±0.41である。部品寸法が平均値53.01、標準偏差0.25の正規分布に従うとき、次の表から求められる不適合品率に最も近い値はどれか。
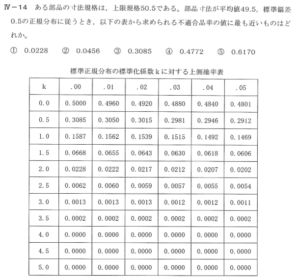
標準正規分布の標準化係数$$k$$に対する上側確率表
| $$k$$ | .00 | .02 | .04 | .06 | .08 |
|---|---|---|---|---|---|
| 0.0 | 0.5000 | 0.4920 | 0.4840 | 0.4761 | 0.4681 |
| 0.2 | 0.4207 | 0.4129 | 0.4052 | 0.3974 | 0.3897 |
| 0.4 | 0.3446 | 0.3372 | 0.3300 | 0.3228 | 0.3156 |
| 0.6 | 0.2743 | 0.2676 | 0.2611 | 0.2546 | 0.2483 |
| 0.8 | 0.2119 | 0.2061 | 0.2005 | 0.1949 | 0.1894 |
| 1.0 | 0.1587 | 0.1539 | 0.1492 | 0.1446 | 0.1401 |
| 1.2 | 0.1151 | 0.1112 | 0.1075 | 0.1038 | 0.1003 |
| 1.4 | 0.0808 | 0.0778 | 0.0749 | 0.0721 | 0.0694 |
| 1.6 | 0.0548 | 0.0526 | 0.0505 | 0.0485 | 0.0465 |
| 1.8 | 0.0359 | 0.0344 | 0.0329 | 0.0314 | 0.0301 |
| 2.0 | 0.0228 | 0.0217 | 0.0207 | 0.0197 | 0.0188 |
① 0.0465
② 0.0548
③ 0.0930
④ 0.1013
⑤ 0.1096

解答
正解は 4 になります。
k値(標準化係数)ベースでの問題解説
この問題は、部品の寸法が正規分布に従うとき、規格外となる(不適合品となる)確率=不適合品率を、標準正規分布のk値(標準化係数)を使って求める典型的な品質管理の計算問題です。
寸法規格が「53.02±0.41」、すなわち「52.61~53.43」の範囲内であれば適合品、それ以外は不適合品となります。
部品寸法は平均53.01、標準偏差0.25の正規分布に従うとされています。
このとき、規格外となる確率(不適合品率)を計算し、最も近い選択肢を選ぶのが目的です。
1. k値(標準化係数)とは
k値とは、元のデータを「平均0、標準偏差1」の標準正規分布に変換したときの「標準化された距離」を表します。
計算式は以下の通りです。$$ k = \frac{X – \mu}{\sigma} $$
- $$ X $$:調べたい値(規格の上限や下限)
- $$ \mu $$:平均値
- $$ \sigma $$:標準偏差
2. 問題の数値をk値に変換
- 寸法規格:53.02±0.41 → 下限52.61、上限53.43
- 平均値:53.01
- 標準偏差:0.25
下限のk値$$ k_L = \frac{52.61 – 53.01}{0.25} = \frac{-0.40}{0.25} = -1.6 $$
上限のk値 $$k_U = \frac{53.43 – 53.01}{0.25} = \frac{0.42}{0.25} = 1.68 $$
3. k値を使って上側確率表から規格外確率を求める
標準正規分布の上側確率表は「そのk値より大きい確率」を示します。
- $$ k = -1.6 $$ の場合、標準正規分布の性質から「左端の確率」=「k=1.6の右端の確率」と同じです。
- $$ k = 1.68 $$ の場合、そのまま表で上側確率を調べます。
表より:
- $$ k = 1.60 $$ → 0.0548
- $$ k = 1.68 $$ → 0.0465
4. 不適合品率の計算
不適合品率は「下限未満」と「上限超え」の両側の合計です。$$ \text{不適合品率} = 0.0548 + 0.0465 = 0.1013 $$
5. 選択肢との照合
選択肢④「0.1013」が計算値と一致します。
各選択肢の詳細解説
① 0.0465
これはk=1.68の上側確率のみ。両側分にはなりません。
② 0.0548
これはk=1.60の上側確率のみ。両側分にはなりません。
③ 0.0930
両側の合計に近いですが、実際の計算値よりやや小さいです。
④ 0.1013
下限未満と上限超えの合計で、計算値と一致します。
⑤ 0.1096
両側の合計としてはやや大きすぎます。
図解イメージ

まとめ:k値活用の要点
- k値を使うことで、どんな平均・標準偏差のデータでも標準正規分布表で確率を調べられる。
- k値で標準化し、上側確率表から規格外の確率(不適合品率)を足し合わせることで、正確な不良率が求まる。
- 本問の答えは「0.1013(選択肢④)」。
感想
この手の問題、苦手です。
過去問はこれがありました。
でも過去問でも書いた通り、理解すればまあ簡単ですね。
なのでこの解説、いつもより時間をかけてじっくり書きました。
これでワタクシはわかった、はず!









