問題
Ⅲ-8 以下のa~dの条件で行っているライン生産に関する次の記述のうち、最も不適切なものはどれか。
【条件】
a.下図の円内の数字は作業要素の識別番号、円外の数字は作業要素の時間を表している。また、円を結ぶ矢印は作業要素の先行関係を示している。
b.作業要素は表に示されているように3工程又は4工程に割り当てられる。
c.各工程での最大の作業時間をサイクルタイムとして運用する。
d.各工程の作業者数は、それぞれ1名である。
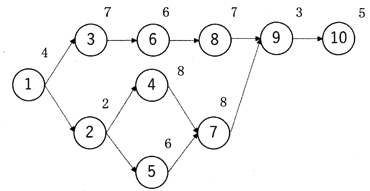
3工程案
| 工程 | 作業要素 |
|---|---|
| 1 | 1 2 3 5 |
| 2 | 4 6 7 |
| 3 | 8 9 10 |
4工程案
| 工程 | 作業要素 |
|---|---|
| 1 | 1 2 3 |
| 2 | 4 5 |
| 3 | 6 8 |
| 4 | 7 9 10 |
① 3工程案でのサイクルタイムは22である。
② 3工程案での編成効率は約85%である。
③ 3工程案で作業要素7と8を入れ替えるとサイクルタイムは短くなる。
④ 4工程案でのラインの編成効率は3工程案よりも低い。
⑤ 4工程案で作業要素3と4を入れ替えてもバランスロスは変わらない。

解答
正解は 4 になります。
ライン生産方式の全体解説
ライン生産方式は、製品を複数の作業要素(工程)に分割し、各工程を順番に流していくことで効率的な生産を目指す手法です。
各作業要素には所要時間が設定されており、工程ごとに作業要素を割り当てていきます。
このとき、各工程の作業時間の最大値が「サイクルタイム」となり、全体の生産効率やバランスロス(ムダ時間)に大きく影響します。
サイクルタイムと編成効率
- サイクルタイム:各工程の作業時間のうち最大のもの。これが生産ライン全体のリズムを決める。
- 編成効率:全作業時間の合計を、サイクルタイム×工程数で割った値。効率が高いほどムダが少ない。
問題の前提条件
- 作業要素は10個あり、それぞれ所要時間が決まっている。
- 3工程案と4工程案の2パターンで作業要素を割り当てている。
- 各工程の作業者は1名。
- サイクルタイムは各案で最大の工程作業時間。
各選択肢の詳細解説
① 3工程案でのサイクルタイムは22である。
【検証】
3工程案の各工程の作業要素と時間を合計すると以下の通りです。
| 工程 | 作業要素 | 合計作業時間 |
|---|---|---|
| 1 | 1, 2, 3, 5 | 4+2+7+6=19 |
| 2 | 4, 6, 7 | 8+6+8=22 |
| 3 | 8, 9, 10 | 7+3+5=15 |
最大は22なので、サイクルタイムは22で正しいです。
② 3工程案での編成効率は約85%である。
【検証】
- 全作業時間合計:4+2+7+8+6+6+8+7+3+5=56
- サイクルタイム×工程数:22×3=66
- 編成効率=56÷66≒0.848(約85%)
「約85%」は四捨五入で妥当な表現です。
③ 3工程案で作業要素7と8を入れ替えるとサイクルタイムは短くなる。
【検証】
- 7(8分)と8(7分)を入れ替えると、工程2は8+6+7=21、工程3は8+3+5=16となる。
- 工程1は変わらず19。
- 最大は21で、元のサイクルタイム22より短くなる。
この記述は正しいです。
④ 4工程案でのラインの編成効率は3工程案よりも低い。
【検証】
4工程案の各工程の作業要素と時間を合計すると以下の通りです。
| 工程 | 作業要素 | 合計作業時間 |
|---|---|---|
| 1 | 1, 2, 3 | 4+2+7=13 |
| 2 | 4, 5 | 8+6=14 |
| 3 | 6, 8 | 6+7=13 |
| 4 | 7, 9, 10 | 8+3+5=16 |
- サイクルタイムは16。
- サイクルタイム×工程数:16×4=64
- 編成効率=56÷64≒0.875(約88%)
3工程案の編成効率(約85%)よりも高くなります。
よって、「4工程案の編成効率は3工程案よりも低い」という記述は不適切です。
⑤ 4工程案で作業要素3と4を入れ替えてもバランスロスは変わらない。
【検証】
- 3(7分)と4(8分)を入れ替えると、工程1は4+2+8=14、工程2は7+6=13。
- 工程3、4は変わらず。
- サイクルタイムは16のまま、バランスロス(ムダ時間)は変わらない。
この記述は正しいです。
まとめ:問題の要点と正答
- サイクルタイムや編成効率は、ライン生産の効率化・バランス改善の指標となる。
- 工程の割り当てや作業要素の入れ替えによって、サイクルタイムやバランスロスが変化する。
- 4工程案の編成効率は3工程案よりも高くなるため、「低い」とする記述は不適切である。
本問の正答は「④」
4工程案でのラインの編成効率は3工程案よりも低い、は誤り。
感想
この手の問題は落ち着いて表を書いていけば確実に解ける!!ということを過去問から学んでおります。

単純な足し算なのでサービス問題、と思ってもいいのかも!
今回も正解。最近調子がいいなあ。









