問題
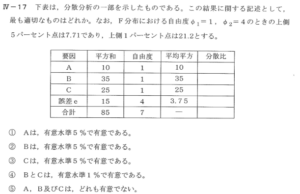
Ⅲ-19 下表は、繰り返しのある場合の二元配置法による分散分析表であり、分散及び分散比は未記入である。この分散分析表に関する次の記述のうち、最も不適切なものはどれか。なお、自由度 φ₁、φ₂、上側確率αパーセント点を F(φ₁, φ₂, α) とすると、F(1, 8, 0.05) = 5.32、F(1, 8, 0.01) = 11.3、F(3, 8, 0.05) = 4.07、F(3, 8, 0.01) = 7.59 である。
| 要因 | 平方和 | 自由度 | 分散 | 分散比 |
|---|---|---|---|---|
| 水質 A | 40 | 1 | ||
| 添加剤 B | 216 | 3 | ||
| 交互作用A×B | 120 | 3 | ||
| 誤差 e | 64 | 8 | ||
| 合計 | 440 | 15 |
① 要因Aの水質については、有意水準5%で有意である。
② 要因Bの添加剤については、有意水準1%で有意である。
③ 交互作用A×Bについては、有意水準5%で有意である。
④ 要因Bの添加剤の分散は、72である。
⑤ 交互作用A×Bの分散比は、5.0である。

解答
正解は 1 になります。
二元配置分散分析(繰り返しあり)の全体解説
分散分析(ANOVA)は、多群間の平均値の差を統計的に検証する方法です。
今回の問題は「二元配置分散分析(繰り返しあり)」で、水質(A)と添加剤(B)、そしてその交互作用(A×B)の主効果と誤差について、統計的な有意性や分散・分散比を考えます。
用語のポイント
- 平方和(Sum of Squares, SS):変動の大きさ。要因ごとのばらつきや、誤差の合計。
- 自由度(df):データの独立した情報量。
- 分散(Mean Square, MS):平方和を自由度で割ったもの。MS=SS/df
- 分散比(F値, F-ratio):要因の分散を誤差の分散で割ったもの。F=MS(要因)/MS(誤差)
- 有意水準:帰無仮説(差がない)を棄却する閾値。5%や1%がよく使われる。
- 上側確率点F(φ₁, φ₂, α):自由度φ₁、φ₂、上側有意水準αのときのF分布の臨界値。
各要素の計算手順
1.分散(MS)の計算
MS=SS/df
- 水質A:MS_A=40/1=40
- 添加剤B:MS_B=216/3=72
- 交互作用A×B:MS_AB=120/3=40
- 誤差e:MS_e=64/8=8
2.分散比(F値)の計算
F=MS(要因)/MS(誤差)
- 水質A:F_A=40/8=5
- 添加剤B:F_B=72/8=9
- 交互作用A×B:F_AB=40/8=5
3.F値の判定(有意性の検定)
F値が、その自由度φ₁, φ₂でのF分布の臨界値を超えれば有意と判定。
- F(1, 8, 0.05)=5.32
- F(1, 8, 0.01)=11.3
- F(3, 8, 0.05)=4.07
- F(3, 8, 0.01)=7.59
各選択肢の詳細解説
① 要因Aの水質については、有意水準5%で有意である。
- F_A=5
- 臨界値: F(1, 8, 0.05)=5.32
- F_A (5) < 臨界値 (5.32)
→ よって有意ではない。
この記述は「不適切」(正解)。
② 要因Bの添加剤については、有意水準1%で有意である。
- F_B=9
- 臨界値: F(3, 8, 0.01)=7.59
- F_B (9) > 臨界値 (7.59)
→ 有意水準1%でも有意。
③ 交互作用A×Bについては、有意水準5%で有意である。
- F_AB=5
- 臨界値: F(3, 8, 0.05)=4.07
- F_AB (5) > 臨界値 (4.07)
→ 有意水準5%で有意。
④ 要因Bの添加剤の分散は、72である。
- 添加剤Bの分散: MS_B=216/3=72
→ 正しい記載。
⑤ 交互作用A×Bの分散比は、5.0である。
- 交互作用A×Bの分散比: F_AB=40/8=5.0
→ 正しい記載。
【まとめ】選択肢と解説
| 記号 | 内容 | 判定 | ポイント |
|---|---|---|---|
| ① | 要因Aは有意水準5%で有意 | 不適切 | F値不足で有意でない |
| ② | 添加剤Bは有意水準1%で有意 | 適切 | F値が1%臨界値超 |
| ③ | 交互作用A×Bは有意水準5%で有意 | 適切 | F値が5%臨界値超 |
| ④ | 添加剤Bの分散は72 | 適切 | MS計算通り |
| ⑤ | 交互作用A×Bの分散比は5.0 | 適切 | F=40/8=5.0 |
【図表】分散分析表の完全版
| 要因 | 平方和 (SS) | 自由度 (df) | 分散 (MS) | 分散比 (F) |
|---|---|---|---|---|
| 水質A | 40 | 1 | 40 | 5.0 |
| 添加剤B | 216 | 3 | 72 | 9.0 |
| 交互作用A×B | 120 | 3 | 40 | 5.0 |
| 誤差e | 64 | 8 | 8 | – |
| 合計 | 440 | 15 |
【まとめ・ポイント】
- 分散分析では分散と分散比、臨界値の比較が重要です。
- F値と臨界値の比較で有意差の有無を判定します。
- 各要因の分散や分散比は計算式を確実に押さえましょう。
- 今回の問題は、分散分析の基本概念や計算過程の理解がカギです。
感想
見事に不正解でした。
ワタクシ、この手の問題に弱いのですよね。
子供の頃インフルエンザにかかって算数での割合の授業に出なかったことが原因と思われます。
過去問はこれくらいでした。
このジャンル、増えると苦戦しちゃうな・・・・。









