問題
Ⅲ-4 作業者の習熟に関する次の記述のうち、最も不適切なものはどれか。
① 横軸に作業の繰り返し回数、縦軸に作業時間をとり、作業時間の減少を表した曲線を習熟曲線という。
② 生産の場では、生産数量の増加により、1個当たりの作業時間が早くなることを習熟というが、心理学ではこれを学習という。
③ 精神的・知的判断作業の場合には、習熟はない。
④ 習熟は、作業者個人はもとより、作業者グループ、システム全体にもみられる。
⑤ 対数線形習熟モデルで習熟曲線を両対数グラフに表すと直線になり、その直線の勾配を習熟係数という。

解答
正解は 3 になります。
問題の概要と習熟の考え方
作業現場では、多くの場合、作業を繰り返すうちにどんどん効率が上がり、1回にかかる時間が短くなっていきます。
この現象を「習熟」と呼びます。
経営工学では「作業者の習熟」が生産性やコスト削減、品質向上に密接に関わる重要なテーマです。
「習熟曲線」や「学習モデル」といった専門用語も多く用いられるため、用語の意味をしっかり押さえておきましょう。
各選択肢の詳細解説
① 「横軸に作業の繰り返し回数、縦軸に作業時間をとり、作業時間の減少を表した曲線を習熟曲線という」
解説
これは定義そのものです。
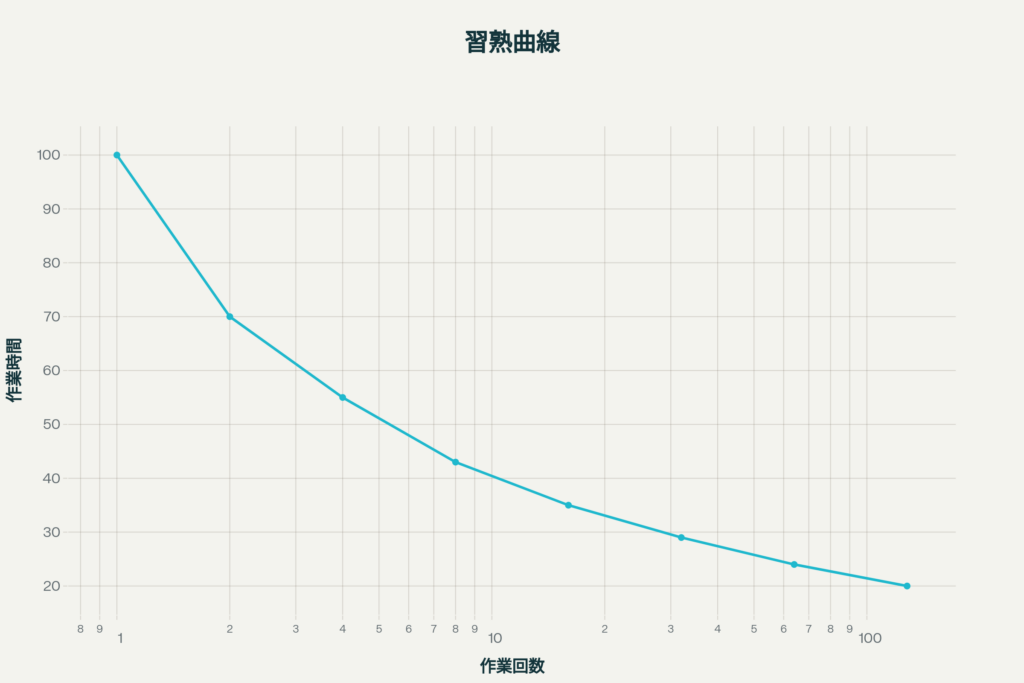
習熟曲線(学習曲線、ラーニングカーブ)は、繰り返し作業と作業時間の関係をグラフで示したものです。
多くの場合、最初は時間がかかりますが、回数を重ねるにつれ作業時間が減少していきます。
例えば「100回繰り返すことで時間が1/2になる」といった特徴を持ちます。
② 「生産の場では、生産数量の増加により、1個当たりの作業時間が早くなることを習熟というが、心理学ではこれを学習という」
解説
生産現場では、同じ作業を繰り返すことで作業者の手際が良くなり、1つあたりの作業時間が短くなります。
この現象を「習熟」または「作業の熟練」と呼びます。
一方で、心理学分野では一般的に「学習」という用語が使われます。
両者は本質的には同じ減少ですが、呼び方の違いがあります。
③ 「精神的・知的判断作業の場合には、習熟はない」
解説
この選択肢が不適切です。
精神的作業や知的判断だけの作業においても「習熟」は十分に存在します。
例えば、複雑な設計業務・論文執筆・経営判断などでも、経験を積み重ねることで判断力やスピード、正確性が向上します。
「頭を使うだけなら慣れはない」などという考えは誤りです。
補足
- 実作業だけでなく、デスクワークや経営判断など多様な領域で「習熟曲線」が観察されます。
④ 「習熟は、作業者個人はもとより、作業者グループ、システム全体にもみられる」
解説
これは正しい内容です。
習熟は個人だけでなく、チーム単位や工程全体でも現れます。
例えば、複数人での作業やライン工程においても、チームワークが熟練することで全体の生産性が高まります。
システムの最適化にも習熟の考え方が応用できます。
⑤ 「対数線形習熟モデルで習熟曲線を両対数グラフに表すと直線になり、その直線の勾配を習熟係数という」
解説
習熟曲線の数学的な性質を説明したものです。
「対数線形モデル」や「両対数グラフ」は、生産工学・品質管理でよく使われる手法です。
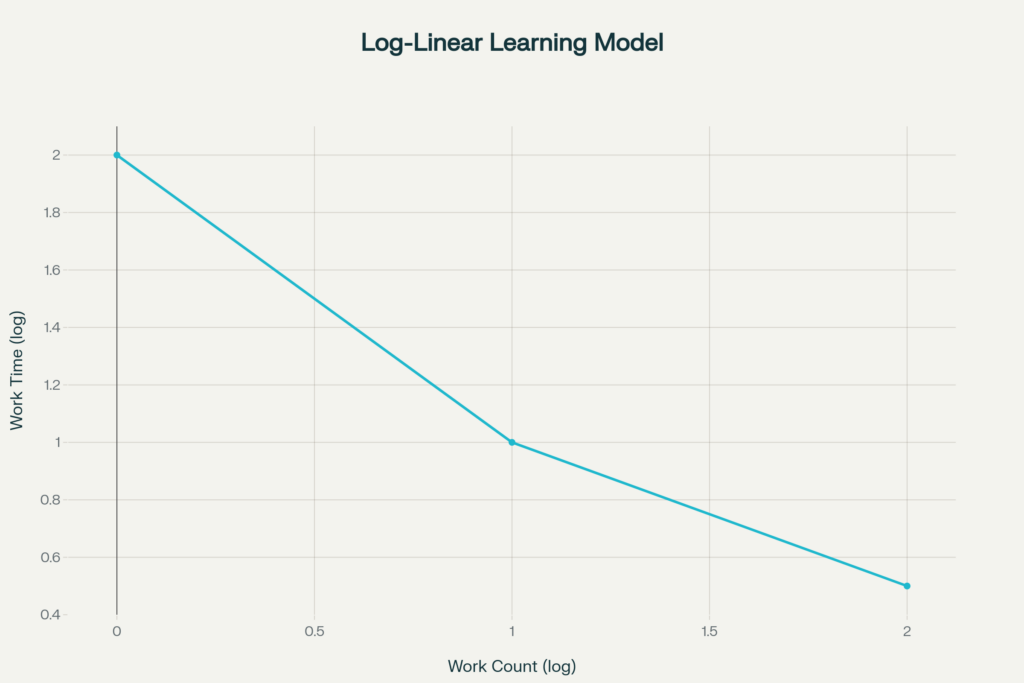
両対数グラフ(横軸・縦軸ともに対数表示)に習熟曲線を描くと、概ね直線的になることが知られています。
この直線の傾きを「習熟係数」と呼び、作業効率の向上具合を定量的に表します。
図表
| 回数(log) | 時間(log) |
|---|---|
| 1 | 10 |
| 10 | 6 |
| 100 | 3 |
→ 両対数グラフで直線になる
まとめ・要点
- 習熟とは、作業の繰り返しによって効率が向上し、作業時間が減少する現象のこと。
- 習熟は肉体的作業にも精神的・知的作業にも現れる。
→「精神的・知的判断作業には習熟がない」というのは誤り。 - 習熟の現象は個人だけでなく、グループや工程全体、システムの最適化にも見られる。
- 習熟曲線は、繰り返し回数と作業時間の関係をわかりやすくグラフ化したもの。
- 対数線形習熟モデルでは両対数グラフ上で直線になる性質があり、その傾きを習熟係数と呼ぶ。
感想
習熟の問題。
今日のは正解でした。
過去問にも似たようなのがありましたから。


このあたり、最近の実務でも出てくるんですよ。
もっともっと、勉強しなきゃと感じ入ります。









