目次
問題
III-13 1種類の製品を生産する職場において、次のa~hの条件の下で、今後4期の能力と負荷のバランスをとって必要最小限の作業者数による生産計画を求めるとき、下記の①~⑤のうち、最も適切なものはどれか。
条件
a. 1つの職場に同一の生産能力をもつ複数の作業者を配置する。
b. 製品1個当たりの標準時間は、0.72時間である。
c. 4期の稼働日数及び需要量は下表のとおりである。
| 期 | 1 | 2 | 3 | 4 | 合計 |
|---|---|---|---|---|---|
| 稼働日数(日) | 19 | 20 | 18 | 17 | 74 |
| 需要量(個) | 1,200 | 1,500 | 2,000 | 1,900 | 6,600 |
d. 1日の実働時間は1人当たり8時間で、稼働率は90%とする。
e. 各期の需要量はその期ごとに満たさなければならない。
f. 第1期の期首在庫量は0とする。
g. 必要最小限の期末在庫は保持してよい。
h. 4期を通して毎日の作業者数は一定とする。
① 第1期の負荷工数は960時間である。
② 第2期の作業者の生産能力は1,440人時である。
③ 第3期の生産量は2,000個である。
④ 4期間合計の負荷工数は5,280時間である。
⑤ 必要最小限の作業者数は9名である。
解答
正解は 5 になります。
必要作業者数の計算
1. 総必要工数の計算
- 総需要量:6,600個
- 1個あたりの標準時間:0.72時間
- 総必要工数:6,600 × 0.72 = 4,752時間
2. 1人当たりの利用可能時間の計算
- 総稼働日数:74日
- 1日の実質作業時間:8時間 × 90% = 7.2時間
- 1人当たりの総利用可能時間:74日 × 7.2時間 = 532.8時間
3. 必要作業者数の計算
- 必要作業者数 = 4,752時間 ÷ 532.8時間 = 8.92人
- 切り上げて9人が必要
各期の生産能力と在庫の確認(9人体制)
第1期
- 生産能力:19日 × 7.2時間 × 9人 ÷ 0.72時間/個 = 1,710個
- 需要:1,200個
- 期末在庫:510個
第2期
- 期首在庫:510個
- 生産能力:20日 × 7.2時間 × 9人 ÷ 0.72時間/個 = 1,800個
- 需要:1,500個
- 期末在庫:810個
第3期
- 期首在庫:810個
- 生産能力:18日 × 7.2時間 × 9人 ÷ 0.72時間/個 = 1,620個
- 需要:2,000個
- 期末在庫:430個
第4期
- 期首在庫:430個
- 生産能力:17日 × 7.2時間 × 9人 ÷ 0.72時間/個 = 1,530個
- 需要:1,900個
- 期末在庫:60個
選択肢の検証
①「第1期の負荷工数は960時間である」
- 実際は1,200個 × 0.72時間 = 864時間
- 不適切
②「第2期の作業者の生産能力は1,440人時である」
- 実際は20日 × 7.2時間 × 9人 = 1,296人時
- 不適切
③「第3期の生産量は2,000個である」
- 実際の生産量は1,620個(期首在庫810個で需要を満たす)
- 不適切
④「4期間合計の負荷工数は5,280時間である」
- 実際は4,752時間
- 不適切
⑤「必要最小限の作業者数は9名である」
- 計算結果と一致
- 適切
したがって、選択肢⑤が最も適切な記述となります。
感想
思ったよりも苦戦しました。
これ、在庫数考慮しないといけないですからね。
解説作ってしまった後見返すと簡単じゃん、なんて思えるのですがなんかうまくいかないところがあったりで紆余曲折でした。
このような表のある問題、案外狙い目なんですよね、ちゃんと計算したら。
これ↓もそうでしたし。
関連記事

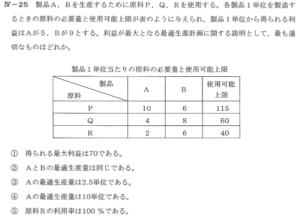
平成24年度 経営工学部門 IV-25
問題 IV-25 製品A、Bを生産するために原料P、Q、Rを使用する。 各製品1単位を製造するときの原料の必要量と使用可能上限が表のように与えられ、製品1単位から得られる利...
見た瞬間、飛ばしたくなる問題ですがまあそうおっしゃらずに、的なものでしょうか。








コメント