平成25年度 経営工学部門 Ⅲ-23PR含む
問題
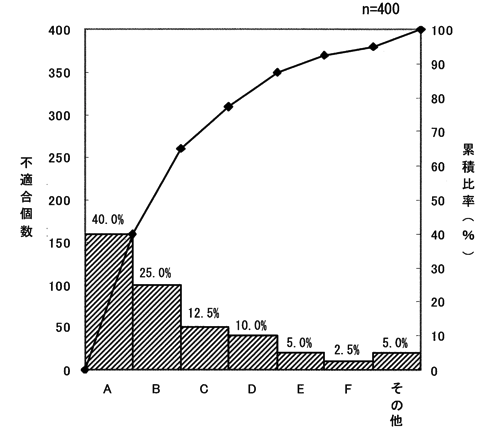
III-23 ある職場において不適合品の発生原因について調査し、以下のようなパレート図を作成した。
現状の不適合品率が1.8%のとき、この図から読み取れる次の記述のうち、最も不適切なものはどれか。
① 棒グラフは、その他を除いてA～F項目は不適合数の降順に並んでいる。
② A、Bの2つの項目を解決すると全体の不適合個数の約65%が解決される。
③ A～D項目までを解決すると、不適合品率が約0.8%に減少する。
④ F項目を解決しても、全体の不適合個数の2.5%にしか影響しない。
⑤ C項目を解決すると、不適合品率が約1.6%となる。
解答
正解は 3 になります。
パレート図を用いた不適合品の原因分析について解説します。
パレート図の読み方
パレート図は、不適合の発生件数を棒グラフで、累積比率を折れ線グラフで表現しています。
主要なポイント
- A〜Fの各項目が不適合の原因を示しています
- 左側の縦軸は不適合個数を表示
- 右側の縦軸は累積比率(%)を表示
- 各項目の発生比率：A(40.0%)、B(25.0%)、C(12.5%)、D(10.0%)、E(5.0%)、F(2.5%)、その他(5.0%)
選択肢①の解説
「棒グラフは、その他を除いてA～F項目は不適合個数の降順に並んでいる」
- 正しい記述です
- A(40.0%) → B(25.0%) → C(12.5%) → D(10.0%) → E(5.0%) → F(2.5%)の順で降順に並んでいます
- 「その他」の5.0%を除けば、完全な降順となっています
選択肢②の解説
「A, Bの2つの項目を解決すると全体の不適合個数の約65%が解決される」
- 正しい記述です
- A(40.0%) + B(25.0%) = 65.0%となり、この2項目の改善で全体の65%が解決されます
選択肢③の解説
「A～D項目までを解決すると、不適合品率が0.8%に減少する」
- 誤った記述です
- A～Dの累積比率は87.5%
- 現状の不適合率1.8%の12.5%(100% – 87.5%)となるため
- 正しい計算結果：1.8% × 0.125 = 0.225%となります
選択肢④の解説
「F項目を解決しても、全体の不適合個数の2.5%にしか影響しない」
- 正しい記述です
- F項目の比率は2.5%であり、そのまま全体への影響度を示しています
選択肢⑤の解説
「C項目を解決すると、不適合品率が1.6%となる」
- 正しい記述です
- C項目の比率は12.5%
- 1.8% × (1 – 0.125) = 1.575%となり、約1.6%になります
計算過程
- 現状の不適合率：1.8%
- A〜Dの累積比率：87.5% (40.0% + 25.0% + 12.5% + 10.0%)
- 改善後の不適合率：1.8% × (100% – 87.5%) = 1.8% × 12.5% = 0.225%
この結果から、A〜D項目を改善することで不適合率を大幅に削減できることがわかります。
重要な考え方
パレート図分析では、「重要な少数」と「重要でない多数」を見極めることが重要です。この場合、上位4項目(A〜D)で全体の約87.5%の問題が解決できることから、これらに注力することが効率的な改善につながります。
感想
パレート図、ずっと前に教育受けたような気が。
この問題もしっかりと計算していけば問題なく解けますね！！
ワタクシは間違っちゃいましたが・・・。
さて、今日から新年ということでページに対するイメージ画像をつけることにしました。
好評だったら過去の投稿も置き換えていこうかな・・・。
関連記事Related articles
