問題
III-25 機械の故障を検知するため、同じ機能をもつ装置S1とS2がある。
これらの装置はそれぞれ以下に示す条件を満たしている。
この2つの装置を組み合わせて下図に示すシステムRを作る。システムRに関する次の記述のうち、最も適切なものはどれか。
条件
a. 装置S1は、機械が故障したときに、故障と知らせる確率が97%である。
b. 装置S2は、機械が故障したときに、故障と知らせる確率が95%である。
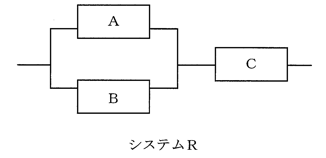
① Aに装置S1、Cに装置S2を用い、Bには装置を接続しないシステムRにおいて、機械が故障したときに、故障と知らせない確率は5%である。
② AとBにS1を用い、Cには装置を接続しないシステムRにおいて、機械が故障したときに、故障と知らせる確率は94.09%である。
③ Aに装置S1、Bに装置S2を用い、Cには装置を接続しないシステムRにおいて、機械が故障したときに、故障と知らせる確率は92.15%である。
④ Aに装置S1、BとCに装置S2を用いたシステムRにおいて、機械が故障したときに、故障と知らせる確率は95%以上である。
⑤ 機械が故障したときに故障と知らせる確率を選択肢④に示したシステムRよりも上げるシステムは、装置S2を2つ使用するだけで作ることができる。
解答
正解は 5 になります。
信頼性工学における直列・並列システムの解説
この問題は、機械の故障検知システムにおける信頼性の計算と、最適なシステム構成を問う問題です。
基本情報の整理
- 装置S1: 故障検知確率97%
- 装置S2: 故障検知確率95%
- システムRは、並列構造(AとB)と直列構造(C)の組み合わせ
確率計算の基本原理
直列構成の場合
- 全ての装置が成功する必要がある
- 成功確率 = P(A成功) × P(B成功)
並列構成の場合
- どちらか一方が成功すれば良い
- 失敗確率 = P(A失敗) × P(B失敗)
各選択肢の分析
選択肢①「A:S1、C:S2、Bなし」
- 直列構成:S1とS2
- 成功確率 = 0.97 × 0.95 = 0.9215(92.15%)
- 失敗確率 = 1 – 0.9215 = 0.0785(7.85%)
- 記述の5%は誤り
選択肢②「A,B:S1、Cなし」
- 並列部分の失敗確率 = 0.03 × 0.03 = 0.0009
- 検知確率 = 99.91%
- 記述の94.09%は誤り
選択肢③「A:S1、B:S2、Cなし」
- 並列部分の失敗確率 = 0.03 × 0.05 = 0.0015
- 検知確率 = 99.85%
- 記述の92.15%は誤り
選択肢④「A:S1、B,C:S2」
- 並列部(A-B)の失敗確率 = 0.03 × 0.05 = 0.0015
- 並列部の成功確率 = 0.9985
- 直列部(C)の成功確率 = 0.95
- 全体の成功確率 = 0.9985 × 0.95 = 0.94858(94.86%)
- 95%以上という記述は誤り
選択肢⑤「S2を2つ並列使用すると」
- 失敗確率 = 0.05 × 0.05 = 0.0025
- 成功確率 = 99.75%
- ④の実際の確率(94.86%)より高い性能を実現
まとめ
システムの信頼性を向上させる場合、単純に高性能な装置を使うだけでなく、適切な配置方法を考えることが重要です。この問題では、性能がやや劣る装置S2でも、並列配置することで高い信頼性を得られることを示しています。
感想
この問題、やたら苦労しました。
④で99.99%になったりして・・・。
要するに並列、直列がよくわかってなかったってことでした。
いや〜、時間かかったなあ。