問題
Ⅲ-21 4種類の立方体の部品A、B、C、Dを横に繋げる作業がある。この部品の寸法は、それぞれ以下の表に示す母平均と母分散の正規分布に従っているものとする。部品A、B、C、Dを横に繋げたときの寸法の母分散として、最も適切なものは次のうちどれか。
| 部品A | 部品B | 部品C | 部品D | |
|---|---|---|---|---|
| 母平均(cm) | 10.0 | 15.0 | 12.0 | 14.0 |
| 母分散(cm²) | 0.3 | 0.2 | 0.6 | 0.5 |
① 0.2
② 0.6
③ 0.8
④ 1.6
⑤ 2.4

解答
正解は 4 になります。
問題の背景と全体像
この問題では、部品A、B、C、Dを横に繋げた際の寸法の母分散を求める必要があります。
母分散は、複数の独立した要素が結合される場合、それぞれの分散を足し合わせることで計算されます。
母分散の計算方法
基本原則
- 独立した変数の和の分散:
独立した変数 \(X_1, X_2, \dots, X_n\) の和 \(Y = X_1 + X_2 + \dots + X_n\) の分散は以下の式で求められます:
\(\text{Var}(Y) = \text{Var}(X_1) + \text{Var}(X_2) + \dots + \text{Var}(X_n)\)
※この性質は変数が独立である場合に適用されます。
問題の条件
- 部品A、B、C、Dの寸法は独立している。
- 各部品の母分散は以下の通り:
- 部品A:0.3
- 部品B:0.2
- 部品C:0.6
- 部品D:0.5
部品を横に繋げた場合
横に繋げると、全体の寸法は各部品の寸法を足し合わせたものになります。
そのため、全体の母分散は以下のように計算されます:
\(\text{Var}_{\text{合計}} = \text{Var}_{\text{A}} + \text{Var}_{\text{B}} + \text{Var}_{\text{C}} + \text{Var}_{\text{D}}\)
計算手順
ステップ1:各部品の母分散を足し合わせる
\(\text{Var}_{\text{合計}} = 0.3 + 0.2 + 0.6 + 0.5\)
ステップ2:合計値を求める
\(\text{Var}_{\text{合計}} = 1.6\)
各選択肢の検証
選択肢① 「0.2」
- 適切性: 不適切
- 理由: 部品Bのみの母分散に該当する値であり、全体の母分散としては不適切。
選択肢② 「0.6」
- 適切性: 不適切
- 理由: 部品Cのみの母分散に該当する値であり、全体の母分散としては不適切。
選択肢③ 「0.8」
- 適切性: 不適切
- 理由: 部品AとBを足し合わせた場合に近い値ですが、全体としては不足しています。
選択肢④ 「1.6」
- 適切性: 適切
- 理由: 計算結果と一致しており、正しい値です。
選択肢⑤ 「2.4」
- 適切性: 不適切
- 理由: 全体の母分散として過剰な値であり、誤りです。
まとめ:技術士試験の重要ポイント
正解:④
正しい計算結果
部品A、B、C、Dを横に繋げた際の寸法の母分散は「1.6」であり、この値が最も適切です。
試験対策ポイント
- 独立した変数の場合、和全体の分散は各変数の分散を足し合わせて求める。
- 母平均や標準偏差ではなく、「母分散」に着目すること。
- 計算ミスを防ぐために各ステップで確認すること。
感想
このての計算は初めてですね。
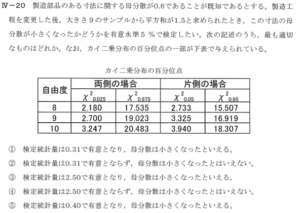
↑のに少し近い感じですが、やっぱり違う。
この手の問題、しっかりと計算したら答えはシンプルなのですよね。
しかしぱっと見うわ、難しい!って思うと解けない・・・・。
地道に解いていきましょう!!









