問題
製造部品のある寸法に関する母分散が0.6であることが既知であるとする。製造工程を変更した後、大きさ9のサンプルから平方和が1.5に求められたとき、この寸法の母分散が小さくなったかどうかを有意水準5%で検定したい。次の記述のうち、最も適切なものはどれか。なお、カイ二乗分布の百分位点の一部が下表で与えられている。
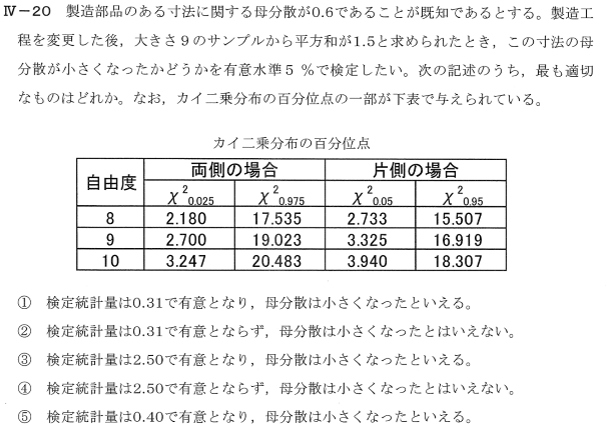
| 自由度 | 両側の場合 | 片側の場合 | ||
| \(χ^{2}_{ 0.025}\) | \(χ^{2}_{ 0.975}\) | \(χ^{2}_{ 0.05}\) | \(χ^{2}_{ 0.95}\) | |
| 8 | 2.180 | 17.535 | 2.733 | 15.507 |
| 9 | 2.700 | 19.023 | 3.325 | 16.919 |
| 10 | 3.247 | 20.483 | 3.940 | 18.307 |
① 検定統計量は0.31で有意となり、母分散は小さくなったといえる。
② 検定統計量は0.31で有意とならず、母分散は小さくなったとはいえない。
③ 検定統計量は2.50で有意となり、母分散は小さくなったといえる。
④ 検定統計量は2.50で有意とならず、母分散は小さくなったとはいえない。
⑤ 検定統計量は0.40で有意となり、母分散は小さくなったといえる。
解答
正解は 3 になります。
この問題は、製造部品のある寸法に関する母分散が変化したかどうかを検定するためのものです。具体的には、製造工程を変更した後の分散が小さくなったかどうかを、カイ二乗分布を用いて検定します。以下に詳しく説明します。
問題の背景
- 母分散: もともとの母集団の分散が0.6であることが知られています。
- 標本分散: 工程変更後のサンプルから得られた標本分散は1.5です。
- 検定の目的: 分散が小さくなったかどうかを5%の有意水準で検定します。
カイ二乗検定とは
カイ二乗検定は、標本分散と母分散を比較して、母集団の分散が特定の値から変化しているかを確認するための手法です。自由度(サンプルサイズ – 1)に基づいてカイ二乗分布を使用します。
検定手順
- 帰無仮説 (\(H_0\)): 母分散は0.6である。
- 対立仮説 (\(H_1\)): 母分散は0.6より小さい。
計算方法
カイ二乗統計量は次の式で計算されます:
$$
\chi^2 = \frac{(n-1) \cdot s^2}{\sigma^2}
$$
ここで:
- \(n\) はサンプルサイズ(自由度 + 1)
- \(s^2\) は標本分散
- \(\sigma^2\) は仮定する母分散
選択肢の解説
なぜ選択肢3が正解であるかの理由を説明します。
- 自由度: 問題文から自由度は9と推測されます(サンプルサイズ10)。
- カイ二乗値: 自由度9の片側検定で有意水準0.05の場合、表からカイ二乗値16.919が得られます。
- 計算結果:
標本分散 \(s^2 = 1.5\)
仮定する母分散 \(\sigma^2 = 0.6\)
カイ二乗統計量 \(\chi^2 = \frac{9 \cdot 1.5}{0.6} = 22.5\)
この22.5は16.919より大きいため、帰無仮説を棄却し、母分散が小さくなったと結論付けます。
検定結果
表から、自由度9で片側検定のカイ二乗値は16.919です。計算されたカイ二乗統計量22.5はこれより大きいため、帰無仮説を棄却します。つまり、母分散は小さくなったと結論付けられます。このように、カイ二乗検定を用いて製造工程の改善効果を統計的に確認することができます。
感想
ぐわ!難しい!!
これは理解しづらいな・・・・。
他の年度の試験問題にも出てくるのだろうか?
何度も何度も解説読んで理解するしかないか・・・・。








コメント