問題
Ⅲ-13 ある職場において発生した400個の不適合品の発生原因について調査し、以下のようなパレート図を作成した。現状の不適合品率が1.5%のとき、この図から読み取れる次の記述のうち、最も不適切なものはどれか。
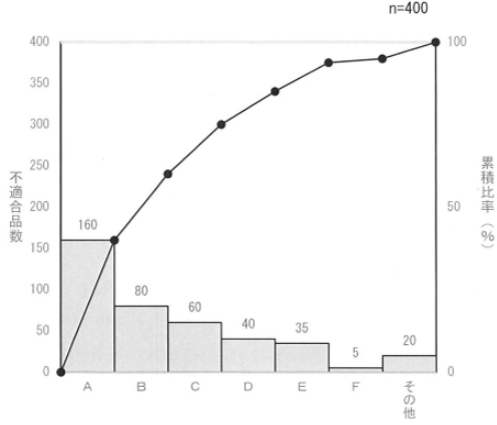
① D項目は、不適合品の10%である。
② A、Bの2つの項目を解決すると全体の不適合品数の約60%が解決される。
③ F項目を解決すると、不適合品率が約1.3%となる。
④ E項目を解決しても、全体の不適合品数の約8.8%にしか影響をしない。
⑤ A~D項目までを解決すると、不適合品率が約0.2%に減少する。

解答
正解は 3 になります。
パレート図と不適合品問題の概要解説
パレート図は、問題の発生原因ごとに件数(または割合)を並べ、累積比率を折れ線グラフで示した図で、「重要な少数(パレートの法則:80対20の法則)」に着目し、優先的に改善すべき項目を特定するのに役立ちます。
本問題では、ある職場で発生した400個の不適合品の発生原因をパレート図で分析し、5つの選択肢から「もっとも不適切な記述」を選びます。
不適合品率は1.5%と設定されています。
パレート図の読み取りポイント
- 横軸:「A」「B」…など、原因の種類
- 縦軸左:不適合品数(0~400個)
- 縦軸右:累積比率(0~100%)
- 棒グラフ:各原因ごとの不適合品数
- 折れ線グラフ:累積比率
画像の棒グラフから、A~Fおよび「その他」までの個数が読み取れます。
| 項目 | 件数 |
|---|---|
| A | 160 |
| B | 80 |
| C | 60 |
| D | 40 |
| E | 35 |
| F | 5 |
| その他 | 20 |
累積で計算しながら、各選択肢を具体的に検討します。
各選択肢の詳細解説
① D項目は、不適合品の10%である。
- D項目の不適合品数は40個。
- 全体400個なので、割合は $$\frac{40}{400} \times 100 = 10\%$$
→ この記述は正しいです。
② A、Bの2つの項目を解決すると全体の不適合品数の約60%が解決される。
- A:160個、B:80個 ⇒ 合計240個
- 割合:$$\frac{240}{400} \times 100 = 60\%$$
→ この記述も正しいです。
③ F項目を解決すると、不適合品率が約1.3%となる。
- F項目の不適合品数は5個。全体の400個から5個減ると395個。
- 不適合品率は全生産数N個に対しての割合。現状は1.5%。
- 不適合品400個=総生産数をN個とすると、 $$0.015N = 400$$ → $$N = 400 / 0.015 = 26,666.\overline{6}$$
- F項目を解決後の不適合品数 395個。 新しい不適合品率は
$$\frac{395}{26,666.\overline{6}} \approx 1.48\%$$
→ 1.3%にはならない。明らかに過大評価。
→ この記述が不適切(正解)です。
④ E項目を解決しても、全体の不適合品数の約8.8%にしか影響をしない。
- E項目は35個
- 割合:$$\frac{35}{400} \times 100 = 8.75\%$$
→ 「約8.8%」は誤差の範囲なので正しい記述です。
⑤ A~D項目までを解決すると、不適合品率が約0.2%に減少する。
- A~D合計:160+80+60+40=340個を削減
- 残るのは400-340=60個
- 新しい不適合品率は
$$\frac{60}{26,666.\overline{6}} \approx 0.225\%$$
→ 「約0.2%」なので正しい記述です。
解説まとめとポイント
- パレート図は「重要な原因への集中改善」のために活用する
- 不適合品率の計算方法や「原因別の個数・割合」の算出は、データ分析の基本
- 不適切な記述は③:「F項目の解決で不適合品率が約1.3%」→実際は1.5%からほとんど変化しない
参考図表イメージ
| 項目 | 不適合品数 | 割合(%) | 累積割合(%) |
|---|---|---|---|
| A | 160 | 40.0 | 40.0 |
| B | 80 | 20.0 | 60.0 |
| C | 60 | 15.0 | 75.0 |
| D | 40 | 10.0 | 85.0 |
| E | 35 | 8.75 | 93.75 |
| F | 5 | 1.25 | 95.0 |
| その他 | 20 | 5.0 | 100.0 |
まとめ
パレート図による「不適合品原因分析」は、品質管理や改善活動の非常に重要な手法です。
選択肢それぞれの裏付け計算も含めて理解し、問題解決力とデータ分析力を身につけましょう。
分析結果の誤認識(今回の「F項目で1.3%」のような)にも注意!
感想
パレート図、苦手ですねえ。
理解をしっかりしていないからですね。


過去問もしっかり解いて再度学ぼう!!









