令和元年度　経営工学部門　Ⅲ-18

問題

Ⅲ－18　ある変量が下図の標準正規分布に従うとき、無作為に抽出された変量を考える。
下図の塗りつぶされた部分の面積をAとしたときの次の記述のうち、最も適切なものはどれか。

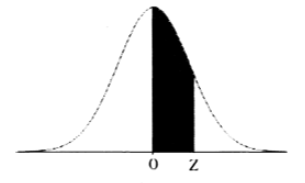
①　変量が０とＺの間の値をとる確率は、２Ａである。

②　変量が－ＺとＺの間の値をとる確率は、Ａである。

③　変量がＺより小さい値をとる確率は、０．５－Ａである。

④　変量が－Ｚより大きい値をとる確率は、０．５＋Ａである。

⑤　変量が－Ｚより小さい値をとる確率は、１－Ａである。

解答

正解は　4　になります。

標準正規分布の基本と本問のポイント

標準正規分布は、平均0、標準偏差1の正規分布です。
グラフは中央が高く左右対称になっており、確率密度関数で表されます。
ある値の範囲における面積は、その範囲に変量が入る確率を示します。
今回の問題では、標準正規分布に従う変数Xについて、0からZまでの範囲の面積（確率）をAとし、Aを使ったさまざまな確率表現の正誤を判別する出題です。

標準正規分布の範囲と面積（確率）との関係

• 標準正規分布のグラフにおいて「面積」は「確率」に等しい。
• 平均（0）の左右、グラフの中心で分布は完全に対称であり、「0からZまで」と「-Zから0まで」の面積は同じ。
• 「0からZまで」の片側の面積をAとおくと、-ZからZまでの面積は2Aに等しい。

各選択肢の詳細解説

① 変量が0とZの間の値をとる確率は、2Aである。

• 解説： 「0からZまで」の確率はA。2Aは「-ZからZまで」の確率となり、「0からZまで」ではありません。誤り。
• ポイント
  • 面積Aは0～Z
  • 2Aは- Z～Z

② 変量が- ZとZの間の値をとる確率は、Aである。

• 解説：「-Zから0まで」の面積もAとなるので、「-ZからZまで」はA + A = 2A。しかし、「A」としているため誤り。
• ポイント
  • -Z～0もA、0～ZもA
  • -Z～Zは2A

③ 変量がZより小さい値をとる確率は、0.5-Aである。

• 解説：Zより小さい＝「左側全体」。0未満の左半分が0.5、0からZまでがAなので、合計0.5 + A。0.5-Aではないので誤り。
• ポイント
  • 左全体＝0.5＋A

④ 変量が- Zより大きい値をとる確率は、0.5＋Aである。

• 解説：「-Zより大きい」は「-Zから+∞」まで。標準正規分布の左半分（0.5）に、「0～Z」（A）が加わるので、0.5＋Aとなり正しい。
• ポイント
  • -Zより大きい＝0.5＋A

⑤ 変量が- Zより小さい値をとる確率は、1-Aである。

• 解説：「-Zより小さい」は、全体（1）から「-Zより大きい」（0.5＋A）を引いたものとなるため、1-（0.5＋A）＝0.5-A。よって誤り。
• ポイント
  • -Zより小さい＝0.5－A

---

まとめ

この問題のポイントは標準正規分布の対称性、確率と面積の関係、そして「0～Z」「-Z～Z」の面積の使い分けです。
それぞれの確率を計算する際は、必ず「どこの範囲の面積か（左右対称性）」「Aが表す範囲」を意識しましょう。

感想

標準正規分布という語句が出る問題は多いのですが、今日のような問題は過去に出ていました。

そうか、ちゃんと解説まで書いたんだけどなあ。

今日も間違いでした。

また解説書いてしっかりと覚えよう。