問題
Ⅲ-19 同じ機能を持つ4つの装置Sがある。これらの装置を組合せた次のシステムのうち、システムの信頼度が3番目に高いものはどれか。
①

②
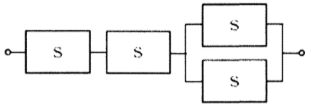
③
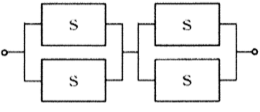
④
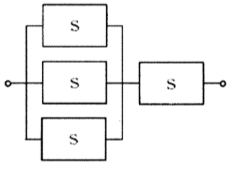
⑤
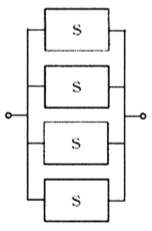

解答
正解は 4 になります。
システム信頼度の基礎
システム信頼度とは、システム全体が正常に動作し続ける確率を示します。
装置(部品)それぞれに故障確率があり、システム全体の構成方法(直列・並列・混合)によって、システムとしての信頼度が大きく変わってきます。
「直列」は全てが正常でないとシステムが動作せず、「並列」はどれか一つが正常なら動作します。
ここが大きなポイントです。
直列システムと並列システム
- 直列システム(Series system)
どれか一つでも故障すると全体が停止します。信頼度は各装置の信頼度を掛け合わせます。
$$R_{series} = R^n$$(R:装置の信頼度、n:台数) - 並列システム(Parallel system)
どれか一つでも動いていれば全体は機能します。信頼度は「全装置が同時に故障する確率」を1から引きます。
$$R_{parallel} = 1 – (1-R)^n$$
混合システム
実際のシステムは直列・並列を組み合わせたものが多数。混合の場合は、部分システムごとに、計算を順次進めていきます。
各選択肢の構成と信頼度の概要
① 完全直列
4つのSが直列に並び、全てが動作しないとシステムは停止します。
- 信頼度
$$R_{series} = R^4$$ - 特徴
一番信頼度が低い組み合わせ。ひとつでも壊れるとアウト。
② 直列+並列
2台直列、次に2台の並列。
- 信頼度
まず後半(並列2台)部分の信頼度:$$1 – (1-R)^2$$
この部分が動作してはじめてシステム全体が動く。前半直列2台部分の信頼度:$$R^2$$
全体:$$R^2 \times [1-(1-R)^2]$$ - 特徴
前段が直列部分なので、完全並列より信頼度は下がる。
③ 並列+直列
2台並列、その後2台直列。
- 信頼度
まず前半(並列2台):$$1-(1-R)^2$$
後半直列2台部分:$$R^2$$
全体:$$[1-(1-R)^2] \times R^2$$ - 特徴
並列部分が前に来ても、直列がどこにあっても理論上は同様。②より信頼度は低くなる。
④ 2段並列構成
2台ずつ並列、それを直列接続。
- 構成図解
[(S||S) — (S||S)]
※S||Sは「2台並列」 - 信頼度
2台並列の単位信頼度:$$1-(1-R)^2$$
それが2つ直列なので:$$[1-(1-R)^2]^2$$ - 特徴
並列で冗長性をもちつつ、直列構成で全体最適化されたバランスタイプ。全体としてかなり高い信頼度となる。
⑤ 4台全並列
全てが並列。
- 構成図解
[S、S、S、Sが全て並列] - 信頼度
$$R_{parallel} = 1-(1-R)^4$$ - 特徴
一番高い信頼度。どれか一つでも動けばOK。
選択肢ごとの詳細解説
① 完全直列(S-S-S-S)
直列構成ではどれか一つが壊れただけでシステム全体が停止します。信頼度Rが高くても、台数が増えると指数的に下がります。たとえばR=0.9なら、
$$0.9^4 = 0.6561$$
非常に脆くなります。
② 直列-並列((S-S)-(S||S))
まず2台が直列になり、この出力が2台並列(どちらか動けばOK)に連結しています。
- 前半直列の信頼度は $$R^2$$
- 後半並列の信頼度は$$1-(1-R)^2$$
全体ではこれを掛け合わせる形となり、信頼度は中程度。
③ 並列-直列((S||S)-(S-S))
前半2台並列(どちらか動けばOK)、その出力を2台直列(両方が動作必要)へ送る構成。
- 並列部分は高い信頼度を持つが、後段の直列で下がる。
- 信頼度は②よりやや劣る。
④ 2段並列&直列((S||S)-(S||S))
2台ずつ並列を2組作り、それを直列につなげた構成。
- 並列でそれぞれ冗長性を確保
- システム全体の信頼度もかなり高く、部分冗長、全体最適とも呼ばれるバランスタイプ
⑤ 完全並列(S||S||S||S)
全台が並列なので、とにかく全員が壊れない限りシステムは生きている状態。
- 信頼度は最大
信頼度の高い順ランキング
各構成でR(装置の信頼度)が十分大きい(例:0.8~0.99)と仮定した場合、以下の通りです。
- ⑤ 完全並列(最も高い)
- ④ 2段並列&直列(バランスタイプ、第二位)
- ② 直列-並列(3番目に高い、設問の答え)
- ③ 並列-直列
- ① 完全直列(最も低い)
まとめ・重要ポイント
今回の問題の鍵となるポイントは、冗長性(Redundancy)とシステム信頼度(Reliability)の違い、そして直列・並列・混合システムの信頼度の考え方です。
直列構成では全てが正常動作必要、並列構成はどれか一つでOK。
バランスタイプの構成はコストと信頼度のバランスが取れ、実際の設計現場で多用されます。
感想
そっくりな問題が過去問にもありました。

なかなかインパクトあったのでこれの解説作った時にちゃんと理解していたようです。
よって今日は正解でしたよ!
やっぱり日々勉強しないと駄目ですねえ。









