問題
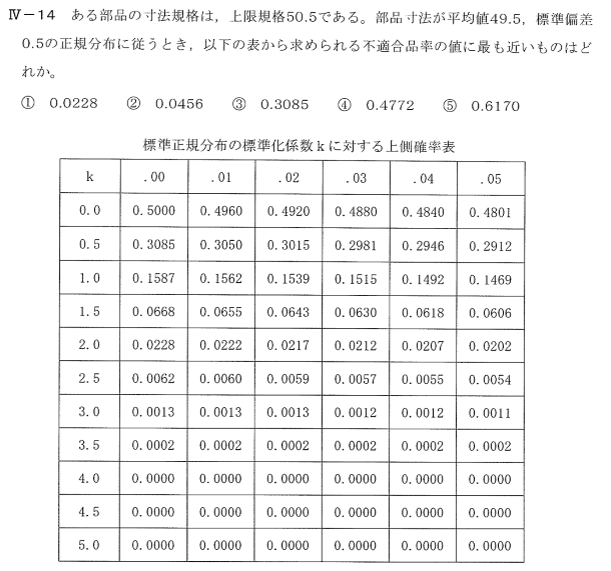
IV-14 ある部品の寸法規格は、上限規格50.5である。
部品寸法が平均値49.5、標準偏差0.50の正規分布に従うとき、以下の表から求められる不適合品率の値に最も近いものはどれか。
① 0.0228 ② 0.0456 ③ 0.3085 ④ 0.4772 ⑤ 0.6170
| k | .00 | .01 | .02 | .03 | .04 | .05 |
|---|---|---|---|---|---|---|
| 0.0 | 0.5000 | 0.4960 | 0.4920 | 0.4880 | 0.4840 | 0.4801 |
| 0.5 | 0.3085 | 0.3050 | 0.3015 | 0.2981 | 0.2946 | 0.2912 |
| 1.0 | 0.1587 | 0.1562 | 0.1539 | 0.1515 | 0.1492 | 0.1469 |
| 1.5 | 0.0668 | 0.0655 | 0.0643 | 0.0630 | 0.0618 | 0.0606 |
| 2.0 | 0.0228 | 0.0222 | 0.0217 | 0.0212 | 0.0207 | 0.0202 |
| 2.5 | 0.0062 | 0.0060 | 0.0059 | 0.0057 | 0.0055 | 0.0054 |
| 3.0 | 0.0013 | 0.0013 | 0.0013 | 0.0012 | 0.0012 | 0.0011 |
| 3.5 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 | 0.0002 |
| 4.0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 4.5 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
| 5.0 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 | 0.0000 |
解答
正解は 1 になります。
この問題は、品質管理における不適合品率の計算に関するものです。
問題の概要
ある部品の寸法に関して:
- 上限規格: 50.5
- 平均値: 49.5
- 標準偏差: 0.50
- 寸法は正規分布に従う
これらの情報を使って、不適合品率を求める問題です。
解説
ステップ1: 標準化
まず、上限規格を標準化します。標準化とは、データを平均0、標準偏差1の標準正規分布に変換することです。
標準化の公式: k = (X – μ) / σ
ここで、X: 上限規格、μ: 平均値、σ: 標準偏差
k = (50.5 – 49.5) / 0.50 = 2.0
ステップ2: 標準正規分布表の利用
問題文に与えられた表は、標準正規分布の上側確率表です。この表を使って、Z値が2.0のときの確率を探します。
表から、k = 2.00のときの値は0.0228です。
ステップ3: 不適合品率の解釈
この0.0228という値は、標準正規分布において、k値が2.0以上となる確率を示しています。つまり、部品の寸法が上限規格50.5を超える確率、すなわち不適合品率を表しています。
結論
したがって、不適合品率は約2.28%(0.0228)となります。
選択肢の中で、この値に最も近いのは①の0.0228です。
補足説明
品質管理では、製品が規格内に収まっているかどうかを確認することが重要です。この問題では、上限規格を超える製品の割合(不適合品率)を求めることで、製造プロセスの品質を評価しています。
不適合品率が低いほど、製造プロセスの品質が高いと言えます。この場合、約2.28%の製品が規格外となっていますが、これが許容できる水準かどうかは、製品の種類や業界の基準によって判断されます。
以上が、この問題の詳細な解説です。統計的な考え方を用いて、製造プロセスの品質を数値化する方法を学ぶことができました。
感想
この手の計算&表問題が出てくるとああ、避けようと思っちゃうのですが。
よくよく調べてみると簡単でした。
もちろん計算式は覚えておく必要がありますが、一発で答えが出るのは気持ちいいですね!
ところで、2.28%の製品が規格外って、あなたの業界ではどう判断されますか??