平成25年度 経営工学部門 Ⅲ-20PR含む
問題
III-20 下表のデータについて、解析用のシューハート管理図によって統計的管理状態にあるか判定したい。
標準値が与えられていない場合のx̄-R管理図を用いて、個々の打点を管理限界線と比較しただけで判定したとき、判定結果に関する次の記述のうち、最も適切なものはどれか。
ただし、下表のデータは、n = 5のサンプルから得られた各群の平均値x̄と範囲Rであり、管理図の管理限界線に関する係数は次のとおりとする。
| n | 4 | 5 | 6 |
|---|---|---|---|
| A₂ | 0.729 | 0.577 | 0.483 |
| D₃ | 0.000 | 0.000 | 0.000 |
| D₄ | 2.282 | 2.114 | 2.004 |
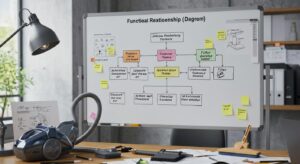
| 群No. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 平均値 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| x̄ | 38.2 | 33.4 | 25.0 | 40.0 | 27.4 | 22.6 | 28.4 | 27.4 | 17.8 | 29.8 | x̄=29.0 |
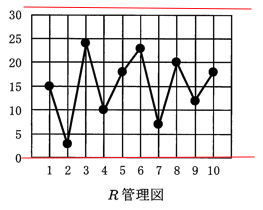
| R | 15 | 3 | 24 | 10 | 18 | 23 | 7 | 20 | 12 | 18 | R̄=15.0 |
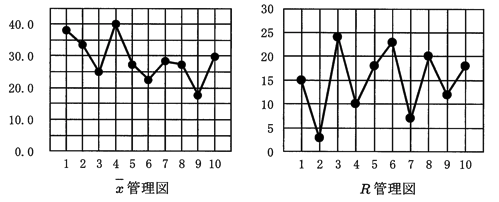
① x̄管理図及びR管理図のいずれもすべての打点が管理限界線の内にあり、当該データは統計的管理状態にある。
② R管理図で異常は見られないが、x̄管理図から、群No.4の打点だけが上方管理限界の外にあり、当該データは統計的管理状態にない。
③ R管理図で異常は見られないが、x̄管理図から、群No.1と群No.4の打点だけが上方管理限界の外にあり、当該データは統計的管理状態にない。
④ R管理図で異常は見られないが、x̄管理図から、群No.1と群No.4の打点だけが上方管理限界の外に、群No.9の打点だけが下方管理限界の外にあり、当該データは統計的管理状態にない。
⑤ R管理図で群No.3の打点だけが上方管理限界の外にあり、また、x̄管理図から、群No.1と群No.4の打点だけが上方管理限界の外に、群No.9の打点だけが下方管理限界の外にあり、当該データは統計的管理状態にない。
解答
正解は 4 になります。
シューハート管理図による品質管理について解説していきます。
シューハート管理図の基本
管理図の種類と目的
- x̄管理図：データの平均値の変動を監視
- R管理図：データのばらつき（範囲）を監視
与えられた条件
- サンプルサイズ：n = 5
- データ：10群の平均値（x̄）と範囲（R）
- 全体の平均値：x̄ = 29.0
- 平均範囲：R̄ = 15.0
管理限界線の計算
係数（n = 5の場合）
- A₂ = 0.577
- D₃ = 0.000
- D₄ = 2.114
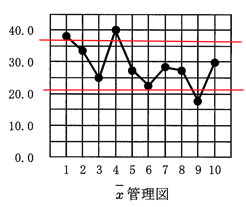
x̄管理図の管理限界
- 上方管理限界（UCL）= x̄ + A₂R̄ = 29.0 + (0.577 × 15.0) = 37.66
- 下方管理限界（LCL）= x̄ – A₂R̄ = 29.0 – (0.577 × 15.0) = 20.34
R管理図の管理限界
- 上方管理限界（UCL）= D₄R̄ = 2.114 × 15.0 = 31.71
- 下方管理限界（LCL）= D₃R̄ = 0.000 × 15.0 = 0
データの分析結果
x̄管理図の異常点
- 群No.1（38.2）：上方管理限界超過
- 群No.4（40.0）：上方管理限界超過
- 群No.9（17.8）：下方管理限界超過
R管理図
すべての点が管理限界内にあり、異常は見られません。
各選択肢の詳細解説
① について
「すべての打点が管理限界線の内にある」という判断は誤りです。x̄管理図で明らかに3点が管理限界を超えています。
② について
群No.4だけでなく、群No.1も上方管理限界を超過し、群No.9が下方管理限界を下回っているため、不適切です。
③ について
群No.9の下方管理限界超過を見落としているため不適切です。
④ について（正解）
- R管理図の判断が正確（異常なし）
- x̄管理図のすべての異常点を正確に指摘
- 統計的管理状態にないという結論も正しい
⑤ について
R管理図で群No.3が管理限界を超えているという判断は誤りです。実際には管理限界内（24 < 31.71）です。
まとめ
このデータは統計的管理状態にありません。その理由は：
- x̄管理図で3つの点が管理限界を超えている
- これは工程に特殊原因が存在することを示している
- プロセスの改善が必要な状態である
感想
シューハート管理図、今までは語句で登場してきました。
今回はいよいよ計算もの！ということで身構えました。
上方管理限界（UCL）、下方管理限界（LCL）、係数の関係を把握しておく必要がありますね。
計算自体はシンプルですが、なかなか解説作成に苦労しました。
もう覚えた！！
関連記事Related articles
