平成27年度　経営工学部門　Ⅲ-25

• Facebook
• X(旧:Twitter)
• はてブ
• LINE
• Pocket

問題

Ⅲ－25 次のうち、輸送問題の解法の1つであるネットワークアルゴリズムを応用して解くことができる問題として最も不適切なものはどれか。

①　最大流量の問題
②　最短路の問題
③　ゲーム理論の問題
④　積み換えの問題
⑤　割当の問題

解答

正解は　3　になります。

問題の概要

この問題は、輸送問題の解法として用いられるネットワークアルゴリズムを応用して解くことができる問題について問うものです。
ネットワークアルゴリズムは、グラフ理論を基にした数理最適化手法であり、輸送や物流、通信などの分野で広く活用されています。
選択肢の中から「最も不適切なもの」を選ぶ必要があります。

ネットワークアルゴリズムの基本知識

ネットワークアルゴリズムとは？

ネットワークアルゴリズムは、グラフ構造を用いて最適化問題を解く手法です。グラフは頂点（ノード）と辺（エッジ）で構成され、以下のような典型的な問題に対応します：

• 最短路問題：2点間の最短経路を求める。
• 最大流問題：ネットワーク上で流量を最大化する。
• 最小費用流問題：流量を一定とした場合のコストを最小化する。
• 割当問題：資源と仕事の割り当てを最適化する。

これらは輸送問題や物流計画、通信ネットワーク設計などで重要な役割を果たします。

各選択肢の詳細解説

① 最大流量の問題

• 解説：
  • 最大流量問題（Maximum Flow Problem）は、供給地から需要地までのネットワーク上で「流量」を最大化する問題です。
  • 例えば、物流ネットワークにおいて、ある出発地から目的地まで運べる最大量を求める際に使用されます。
  • ネットワークフローアルゴリズム（例：フォード・ファルカーソン法）が適用可能です。
• 結論：この記述は正しいです。

② 最短路の問題

• 解説：
  • 最短路問題（Shortest Path Problem）は、ネットワーク上で2点間の経路の中で「コストが最小となる経路」を求める問題です。
  • 例えば、カーナビが出発地から目的地までの最短経路を計算する際に使われます。
  • ダイクストラ法やベルマン・フォード法などが代表的なアルゴリズムです。
• 結論：この記述は正しいです。

③ ゲーム理論の問題

• 解説：
  • ゲーム理論は、複数のプレイヤーが戦略的に意思決定を行う状況を分析する理論です。ナッシュ均衡や協力ゲームなどが含まれます。
  • ゲーム理論はネットワーク構造を考慮した「グラフィカルゲーム」などにも応用されますが、基本的にはネットワークフローアルゴリズムとは異なるアプローチです。
  • 輸送問題やネットワークフローとは直接関係しないため、この記述は不適切です。
• 結論：この記述は誤りです（正解）。

④ 積み換えの問題

• 解説：
  • 積み換え問題（Transshipment Problem）は、輸送途中で積み替え地点を考慮しながら最適な輸送計画を立てる問題です。
  • ネットワークフローアルゴリズムによって効率的に解くことが可能です。例えば、港湾や倉庫間で荷物を積み替える際のコスト最小化が該当します。
• 結論：この記述は正しいです。

⑤ 割当の問題

• 解説：
  • 割当問題（Assignment Problem）は、資源とタスクを1対1で割り当てる際に総コストや作業時間を最小化する問題です。
  • この問題は二部グラフマッチングとして定式化でき、ハンガリアン法や線形計画法などによって効率的に解けます。また、ネットワークフローアルゴリズムも適用可能です。
• 結論：この記述は正しいです。

問題の要点とまとめ

問題文から導き出した結論

• 正解は ③：「ゲーム理論の問題」が不適切。

ポイントまとめ

1. ネットワークアルゴリズムは、「最大流」「最短路」「積み換え」「割当」など多くの輸送・物流関連問題に適用可能。
2. ゲーム理論は戦略的意思決定を扱う分野であり、ネットワークフローアルゴリズムとは直接関係しないため、不適切と判断されます。

ネットワークアルゴリズムの具体的な応用例

ネットワークアルゴリズムは、輸送、物流、通信、プロジェクト管理など、多くの分野で応用されています。
以下に具体的な応用例をいくつか挙げて解説します。

1. 物流と輸送計画

応用例：配送ネットワークの最適化

• 課題：
  • 倉庫から複数の店舗へ商品を配送する際に、輸送コストを最小化したい。
• 適用アルゴリズム：
  • 最小費用流問題：ネットワーク上で流量を一定とし、輸送コストが最小になるルートを求める。
• 具体例：
  • 倉庫Aから店舗B、C、Dへの配送ルートを設計する際に、道路の距離や通行料金を考慮して最適な配送経路を算出。

2. 通信ネットワーク設計

応用例：最大データ転送量の計算

• 課題：
  • 通信ネットワーク上で、あるサーバーからクライアントまでのデータ転送量を最大化したい。
• 適用アルゴリズム：
  • 最大流問題：ネットワーク上で流量（データ転送量）を最大化する。
• 具体例：
  • インターネットプロバイダーが、サーバーから複数のルーターを経由してクライアントにデータを届ける際に、帯域幅（容量）を考慮して最大転送量を計算。

3. 都市交通計画

応用例：渋滞回避のための交通経路設計

• 課題：
  • 都市内の道路網で、車両が渋滞を避けて目的地に到達する最短経路を見つけたい。
• 適用アルゴリズム：
  • 最短路問題：距離や時間が最小となる経路を求める。
• 具体例：
  • カーナビゲーションシステムが現在地から目的地までの最短ルートをリアルタイムで計算し、渋滞情報も考慮して経路を更新。

4. プロジェクト管理

応用例：プロジェクトスケジュールの最適化

• 課題：
  • プロジェクト内のタスク間の依存関係を考慮し、全体の工期を短縮したい。
• 適用アルゴリズム：
  • クリティカルパス法（CPM）：タスク間の依存関係と所要時間からプロジェクト全体の最短完了時間を求める。
• 具体例：
  • 建設プロジェクトで、基礎工事→骨組み建設→内装工事というタスク間の依存関係を考慮しつつ、全体スケジュールを最適化。

5. 製造業における資源割当

応用例：作業員と機械へのタスク割当

• 課題：
  • 複数の作業員と機械に対してタスクを割り当てる際に、総作業時間やコストを最小化したい。
• 適用アルゴリズム：
  • 割当問題（Assignment Problem）：資源とタスク間の1対1対応で総コストや時間が最小になる組み合わせを求める。
• 具体例：
  • 製造ラインで複数の作業員に異なる工程（溶接、塗装など）を効率的に割り当てる。

6. サプライチェーン管理

応用例：在庫補充と輸送計画

• 課題：
  • サプライチェーン全体で在庫補充と輸送コストを最小化しつつ、需要に対応したい。
• 適用アルゴリズム：
  • 積み換え問題（Transshipment Problem）：中継地点（倉庫や港湾）で積み替えながら輸送コストを最小化する。
• 具体例：
  • 海外から輸入された商品が港湾Aに到着後、複数の倉庫に分配され、その後店舗へ配送される際の全体コスト最小化。

7. 航空ネットワーク設計

応用例：航空便スケジュールの最適化

• 課題：
  • 航空便間で乗客や貨物が効率的に乗り継ぎできるようスケジュールとルートを設計したい。
• 適用アルゴリズム：
  • 最大流問題や積み換え問題が利用可能。
• 具体例：
  • 空港間で貨物便や乗客便が効率的に運行できるよう、乗り継ぎ時間や輸送能力制約を考慮してルート設計。

ネットワークアルゴリズム活用時のメリット

1. 効率的な資源利用：
   • 輸送コストや作業時間などの削減が可能。
2. 柔軟な対応力：
   • 渋滞やトラブル発生時にも迅速な再計算が可能。
3. 可視化による意思決定支援：
   • 問題構造がグラフとして可視化されるため、意思決定が容易になる。

感想

いや〜、これもささっと解説書いて終わりにしようと思っていたのですが。

ネットワークアルゴリズム、よくわからないので追加していろいろ調べました。

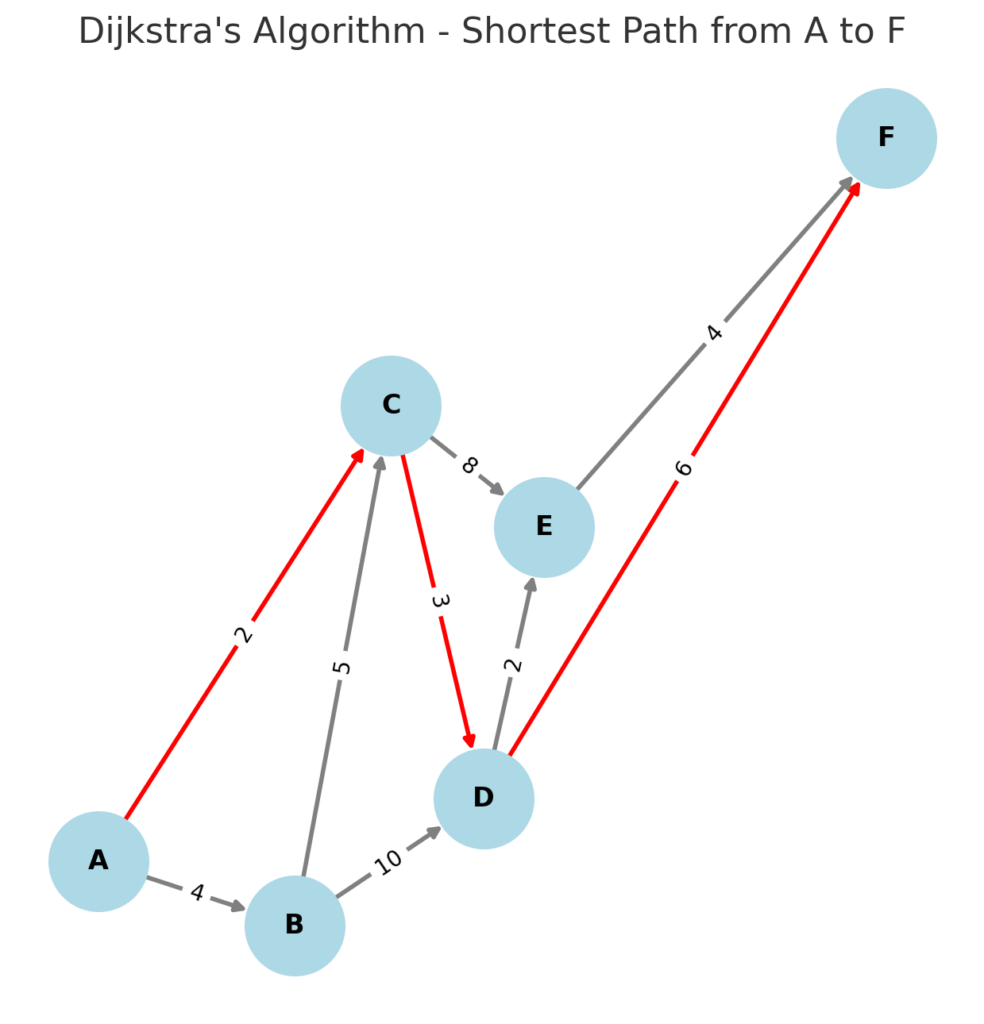
サンプル画像はダイクストラ法のものですが、いろいろ難しそう。

ってか、こういう問題あったよなあ(笑)

すぐに探し出せませんが・・・・。

• Facebook
• X(旧:Twitter)
• はてブ
• LINE
• Pocket