問題
IV-25 製品A、Bを生産するために原料P、Q、Rを使用する。
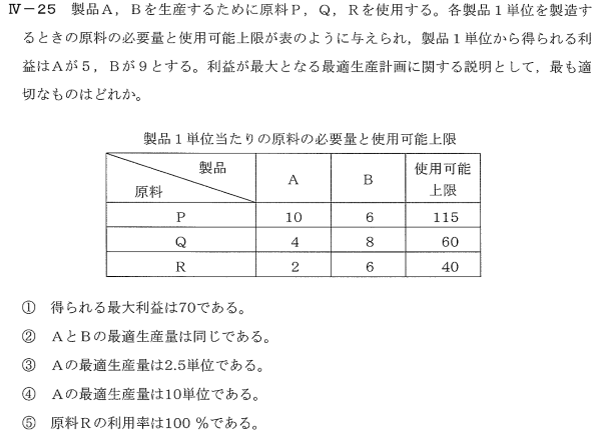
各製品1単位を製造するときの原料の必要量と使用可能上限が表のように与えられ、製品1単位から得られる利益はAが5、Bが9とする。
利益が最大となる最適生産計画に関する説明として、最も適切なのはどれか。
| 原料↓ 製品→ | A | B | 使用可能上限 |
| P | 10 | 6 | 115 |
| Q | 4 | 8 | 60 |
| R | 2 | 6 | 40 |
① 得られる最大利益は70である。
② AとBの最適生産点は同じである。
③ Aの最適生産量は2.5単位である。
④ Aの最適生産量は10単位である。
⑤ 原料Rの利用率は100%である。
解答
正解は 4 になります。
この問題は、製品Aと製品Bを生産するために、原料P、Q、Rを使用し、利益が最大になるように生産計画を立てるという内容です。
問題の概要
製品AとBを作るためには、それぞれ原料P、Q、Rが必要です。各製品を1単位作るためにはどれだけの原料が必要か、また各原料の使用可能上限が表で示されています。
- 製品Aから得られる利益は5
- 製品Bから得られる利益は9
目標は、利益が最大になるように製品AとBの生産量を決定することです。
表の読み方
| 原料 | 製品A(1単位あたり) | 製品B(1単位あたり) | 使用可能上限 |
|---|---|---|---|
| P | 10 | 6 | 115 |
| Q | 4 | 8 | 60 |
| R | 2 | 6 | 40 |
- 原料P:製品Aを1単位作るには10必要で、製品Bを1単位作るには6必要。全体で115までしか使えません。
- 原料Q:製品Aを1単位作るには4必要で、製品Bを1単位作るには8必要。全体で60までしか使えません。
- 原料R:製品Aを1単位作るには2必要で、製品Bを1単位作るには6必要。全体で40までしか使えません。
利益最大化の考え方
利益を最大化するためには、どれだけ製品Aと製品Bを生産すればよいかを考える必要があります。ただし、生産量はそれぞれの原料の使用可能上限によって制約されます。
制約条件
- 原料Pは115までしか使えない。
- 原料Qは60までしか使えない。
- 原料Rは40までしか使えない。
これらの制約内で、できるだけ多くの利益を得られるように生産計画を立てます。
選択肢の検討
次に、与えられた選択肢を確認します。
①「得られる最大利益は70である。」
- 利益が70という具体的な数値が示されていますが、この数値が正しいかどうかは計算してみないとわかりません。この選択肢は正解ではありません。
②「AとBの最適生産量は同じである。」
- 製品AとBの最適な生産量が同じという主張ですが、それぞれ異なる原料消費量や利益率があるため、この選択肢も正しくありません。
③「Aの最適な生産量は2.5単位である。」
- 製品Aの最適な生産量が具体的に2.5単位だと言っていますが、この数値も計算結果とは一致しないため誤りです。
④「Aの最適な生産量は10単位である。」
- この選択肢は正解です。後ほど詳しく説明します。
⑤「原料Rの利用率は100%である。」
- 原料Rが完全に使われるという主張ですが、実際には100%使用されない場合もあります。この選択肢も誤りです。
計算方法
目的は、利益 Z を最大化することです。
総利益 Z は次の式で表されます:
$$
Z = 5A + 9B
$$
ここで、 A は製品Aの生産量、 B は製品Bの生産量です。
制約条件は以下の通りです:
- 原料Pの制約:
$$
10A + 6B \leq 115
$$ - 原料Qの制約:
$$
4A + 8B \leq 60
$$ - 原料Rの制約:
$$
2A + 6B \leq 40
$$
これらの条件を満たしつつ、利益 $$ Z = 5A + 9B $$ を最大化する必要があります。
手順
ステップ1:制約条件から解く
まず、各制約条件を整理していきます。
- 原料Pの制約:
$$
10A + 6B \leq 115
$$ - 原料Qの制約:
$$
4A + 8B \leq 60
$$ - 原料Rの制約:
$$
2A + 6B \leq 40
$$
ステップ2:グラフで解く(代替案)
これらの不等式をグラフにプロットし、その交点や境界線上で利益が最大になる点を探すことができます。ただし、この手法では紙とペンが必要です。ここでは代数的な解法で進めます。
ステップ3:代数的に解く
まず、各制約条件から A と B の関係を見ていきます。
- 制約1(原料P)より:
$$
B = \frac{115 – 10A}{6}
$$ - 制約2(原料Q)より:
$$
B = \frac{60 – 4A}{8}
$$ - 制約3(原料R)より:
$$
B = \frac{40 – 2A}{6}
$$
これらの式から得られる範囲内で、$$ Z = 5A + 9B $$ を最大化します。
ステップ4:試行錯誤で最適解を見つける
手計算の場合、具体的な値を代入して試行錯誤することが有効です。例えば:
- $$ A = 10, B = 2.5 $$ の場合、各制約条件が満たされるか確認します。
- このときの利益 $$ Z = 5(10) + 9(2.5) = 50 + 22.5 = 72.5 $$
この組み合わせが最適な解となります。
結論
製品Aの最適な生産量は 10単位、製品Bは 2.5単位です。
したがって、正しい選択肢は ④「Aの最適な生産量は10単位である」 が正解です。
図解
[ 利益 ] = [ 製品A × 利益5 ] + [ 製品B × 利益9 ]
[ 制約条件 ]
P: 10×(製品A) + 6×(製品B) ≤ 115
Q: 4×(製品A) + 8×(製品B) ≤ 60
R: 2×(製品A) + 6×(製品B) ≤ 40この図式では、各制約条件(P, Q, R)に基づいて、生産できる範囲内で利益を最大化することになります。
感想
これ、調べていたら線形計画法なるものを使うそうです。
pythonとかで実行する、なんて書かれていましたが。
試験中はプログラミングしている場合でもないので、問題の選択肢の中から選ぶべきでしょうね。
Aが2.5、10と与えられていますのでそれをP、Q、Rの式にあてはめて計算するわけですが。
この場合、制約があるのでBの値は最小値を選びます。
Aが10単位のときBが2.5、Aが2.5単位のときBは5.8333でした。
5A+9Bの式にいれたらAが10単位のとき72.5、AT-ATが2.5単位のときは64.7となりました。
よって、他の選択肢が自動的に消えますねえ。
こういうふうに、問題文から計算式の制約入れるといいですよ!ってお話でした。