平成24年度 経営工学部門 IV-24PR含む
問題
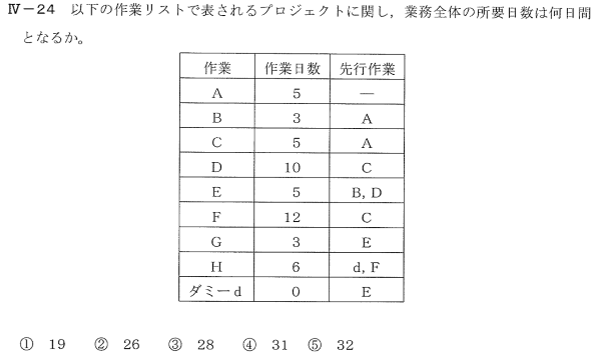
IV-24 以下の作業リストで表されるプロジェクトに関し、業務全体の所要日数は何日間となるか。
| 作業 | 作業日数 | 先行作業 |
| A | 5 | － |
| B | 3 | A |
| C | 5 | A |
| D | 10 | C |
| E | 5 | B、D |
| F | 12 | C |
| G | 3 | E |
| H | 6 | d、F |
| ダミーd | 0 | E |
① 19
② 26
③ 28
④ 31
⑤ 32
解答
正解は 4 になります。
この問題は、プロジェクト管理の一つである「クリティカルパス法（Critical Path Method, CPM）」を使って、プロジェクト全体の所要日数を求めるものです。手順を一つずつ解説していきます。
1. 問題の概要
表には、各作業（A～Hおよびダミー作業d）、その作業にかかる日数、そして先行する作業が示されています。ここで「先行作業」とは、その作業を始める前に完了していなければならない作業のことです。この情報をもとに、プロジェクト全体が完了するまでに何日かかるかを求めます。
2. クリティカルパスとは？
クリティカルパスとは、プロジェクトの全体の所要日数を決定する最も時間がかかる経路のことです。この経路上の作業は「クリティカル作業」と呼ばれ、これらの作業が遅れるとプロジェクト全体も遅れてしまいます。
3. 作業の依存関係を整理する
まず、各作業の依存関係（どの作業がどれに続くか）を整理します。以下のように表を読み解きます：
- A: 5日間、先行作業なし
- B: 3日間、Aが終わった後
- C: 5日間、Aが終わった後
- D: 10日間、Cが終わった後
- E: 6日間、B、Dが終わった後
- F: 12日間、Cが終わった後
- G: 3日間、Eが終わった後
- H: 6日間、d、Fが終わった後
- ダミーd: ダミー作業（0日）、Eが終わった後
4. ネットワーク図を描く
次に、この依存関係を基にネットワーク図（フローチャート）を描きます。以下はその図のイメージです。
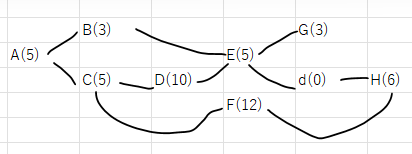
5. 各経路の日数を計算する
次に、このネットワーク図から各経路の日数を計算します。経路ごとにスタートからゴールまでの日数を合計します。
経路1: A → B → E → G
- A = 5日
- B = 3日
- E = 5日
- G = 3日
合計：5 + 3 + 5 + 3 = 16日
経路2: A → B → E → d → H
- A = 5日
- B = 3日
- E = 5日
- d = 0日
- H = 6日
合計：5 + 3 + 5 + 0 + 6 = 19日
経路3: A → C → D → E → G
- A = 5日
- C = 5日
- D = 10日
- E = 5日
- G = 3日
合計：5 + 5 + 10 + 5 + 3 = 28日
経路4: A → C → D → E → d → H
- A = 5日
- C = 5日
- D = 10日
- E = 5日
- d = 0日
- H = 6日
合計：5 + 5 + 10 + 5 + 0 + 6 = 31日
経路5: A → C → F → H
- A = 5日
- C = 5日
- F = 12日
- H = 6日
合計：5 + 5 + 12 + 6 = 28日
6. 最長経路（クリティカルパス）を見つける
上記の経路の中で最も長い時間がかかる経路は「経路4」であり、その所要時間は31日です。このため、この経路がクリティカルパスとなります。
感想
ネットワーク図、汚くてスミマセン。
全然答えが合わなくて、急いでエクセルで作っていたもので。
そしたら、表を間違って作っていたことが判明。
最長38日とかになってましたからね、冷や汗かきました。
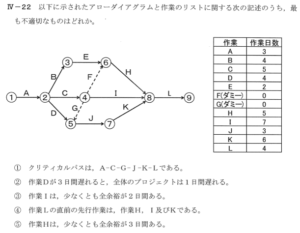
この問題と似ていましたね！
あ、タミーは破線になるのか・・・。
関連記事Related articles
