平成24年度 経営工学部門 IV-20PR含む
問題
IV－20 製造部品のある寸法に関する母分散は0.6であることが既知であるとする。
製造工程を変更した後、大きさ9のサンプルから平方和が1.5と求められたとき、この寸法の母分散が小さくなったかどうかを有意水準5％で片側検定したい。
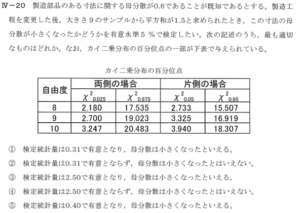
次の記述のうち、最も適切なものはどれか。なお、カイ二乗分布の百分位点の一部が下表で与えられている。
| 自由度 | χ²0.05 | χ²0.95 |
| 8 | 2.733 | 15.507 |
| 9 | 3.325 | 16.919 |
| 10 | 3.940 | 18.307 |
① 検定統計量は0.31で有意となり、母分散は小さくなったといえる。
② 検定統計量は2.50で有意となり、母分散は小さくなったといえる。
③ 検定統計量は2.50で有意とならず、母分散は小さくなったとはいえない。
④ 検定統計量は15.0で有意となり、母分散は小さくなったといえる。
⑤ 検定統計量は15.0で有意とならず、母分散は小さくなったとはいえない。
解答
正解は 2 になります。
まず、この問題は「母分散の検定」という統計学の手法を使います。簡単に言うと、製造部品のばらつき具合が本当に小さくなったかどうかを確かめる方法です。
問題の設定
- 元々の母分散：0.6（これが「既知」という意味）
- サンプルの大きさ：9
- 平方和：1.5
- 検定の種類：片側検定（「小さくなったかどうか」を調べるため）
- 有意水準：5%（0.05）
検定統計量の計算
検定統計量は以下の式で計算します：
$$
\chi^2 = \frac{(n-1) \cdot s^2}{\sigma^2}
$$
ここで、
\(n\)：サンプルの大きさ（9）
\(s^2\)：不偏分散（平方和 / (n-1) = 1.5 / 8 = 0.1875）
\(\sigma^2\)：元々の母分散（0.6） χ² = 8 * 0.1875 / 0.6 = 2.5
判断基準
自由度 =\((n-1) \) = 8 のとき、
χ²0.05 = 2.733（表から） 片側検定で「小さくなったか」を調べるので、
計算した値 < 2.733 なら「有意」（つまり、小さくなったと言える）
判断
計算した値：2.5 < 2.733
よって、有意となり、母分散は小さくなったと言えます。
図解：
2.5 2.733 ↓ ↓0 ---+-----+-----> | | 計算値 χ²0.05 ←有意→|←有意でない→この図で、計算値が左側（小さい方）にあるので、「有意」となります。
結論：
検定統計量は2.50で有意となり、母分散は小さくなったと言えます。
したがって、正解は選択肢②です。
この問題は、製造工程の改善が本当に効果があったかどうかを統計的に確認する方法を示しています。このような手法は、品質管理や生産性向上など、経営工学の様々な場面で活用されています。
感想
改善、大事ですね！
そしてこのχ²分布は毎年出るようです。
ここでも書いたのですが、なんだか理解しづらいような・・・・。
来年の問題では解けるだろうか？？
まずは公式がスラスラ出てくるようにしておかないと。
関連記事Related articles
